Mailing lists on the Internet are the community where people discuss various topics via E-mail. In this paper, we aim at discovering influential comments stimulating peoples' interest by mining the archives of mailing lists. Here we employ Influence Diffusion Model (IDM) in text-based communication, where the influence of comments are defined as the degree of text-based relevance of messages.
Influence Diffusion Model, mining mailing list archives
Diffusion research has been attracted research attentions for decades. In the 1950's and 1960's, Katz et al. [1] and Rogers [2] proposed some diffusion models from mass media to people. Shifting our focus into the diffusion on text-based communication, the researches of computer mediated communications (CMC) [3][4] are deeply relevant. Shibanai et al. analyzed the diffusion process of `Pentium bug in 1994' by questionnaires [5]. Bordia et al. studied rumor transmission chains by classifying the content of individual messages [6]. Kaneko et al. analyzed the comment-chain of e-mails in a mailing-list by using network analysis methods to discover influential comments/people [7]. The study used only the structure of comment-chain, not used the contents.
In this paper, we aim at discovering influential comments stimulating peoples' interest by using not only the structure of comment-chain, but also the contents. In the Section 2, we first propose Influence Diffusion Model (IDM) in text-based communication, where the influence of comments are defined as the degree of text-based relevance of messages. Then, we apply this model to the archives of a mailing list, and present our discoveries in Section 3.
In a mailing list, communications between people are done by exchanging comments, i.e., posting new comments or replying to the comments. Our first assumption is that the relations of comments, called comment-chain, show the flow of influence. For example, if comment Cy replies to comment Cx, it is considered that Cy is affected by Cx. That is, the influence diffuses from Cx to Cy. In this way, the influence diffuses throughout the comment-chain. Our second assumption is that people's idea is expressed and propagated by the medium of terms. Therefore, the process of diffusion of influence is defined as follow.
Definition 1 In text-based communication, influence diffuses along the comment-chain by medium of terms, i.e., words or phrases.We define the influence by the degree of terms propagating through the comment-chain. For example, If Cy replies to Cx, the influence of Cx onto Cy, ix, y, is defined as
ix, y = | wx ∩ wy | / | wy | ,
where wx and wy are the set of terms in Cx and Cy respectively. In addition, if Cz replies to Cy, the influence of Cx onto Cz via Cy, ix, z, is defined as
ix, z = | wx ∩ wy ∩ wz | / | wz | × ix, y ,
where wz are the terms in Cz. It is considered that the more a comment affects other comments, the more the influence increases. The influence of a comment comes to be measurable.
Definition 2 The influence of a comment to the community is measured by the sum of influence diffused from the comment to all other members of the community.Applying Definition 2 to Cx, the influence is measured by the sum of influence diffused from Cx, i.e., ix, y + ix, z if the community has three members x, y and z.
We formalize the influence of a comment Ci. The influence of Ci diffuses along the comment-chain by the medium of terms Definition 1, and the influence is measured by the sum of influence diffused from Ci (Definition 2). Here, let ξi, z be the comment-chain which starts from Ci, i.e., ξi, z = { Ci, Cj, Ck … Cq, Cr … Cy, Cz } { i < j < k … q < r … y < z }, and the influence of Ci onto Cr be ii, r. Then, ii, r is described as
ii, r = | wi ∩ wj ∩ … ∩ wr | / | wr | × ii, q ,
where | wr | denotes the count of terms in Cr, and | wi ∩ wj ∩ … ∩ wr | denotes the count of propagated terms from Ci to Cq. ii, r means that ii, q affects ii, r in proportion to the count of propagated terms from Ci to Cr in the count of terms in Cr. Here, let Iξi, z be the sum of influence diffused from Ci in ξi, z. Then, Iξi, z is described as
Iξi, z = ii, j + ii, k + … + ii, y + ii, z .
The influence of Ci is defined as the sum of Iξ for all comment-chains from Ci (each comment-chain denotes ξ, for example). Let Pi be all comment-chain which start from Ci, and the influence of Ci be DCi. Then, DCi is described as
DCi = ∑ξ ∈ Pi Iξ .
We apply IDM proposed in Section 2 to a part of comment-chain in a mailing list managed in our laboratory. The comment-chain we use here is composed of 24 comments, and the main topic is a lecture on text-mining and natural language processing tools.
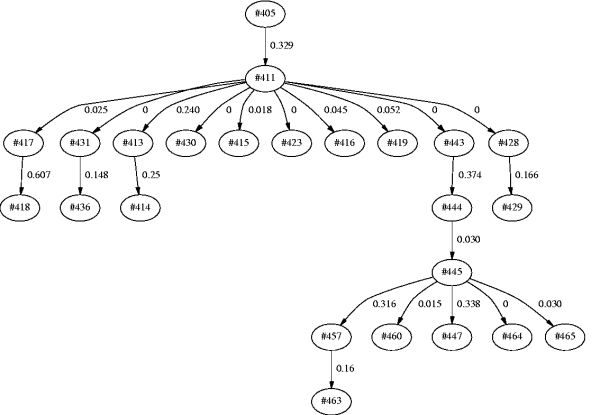
The flows of influence between comments are shown in Fig.1, and the top 5 comments in the order of values of diffusing influence (DC) are shown in Table 1.
| Ranking | Comment ID | DC |
| 1 | #445 | 0.700 |
| 2 | #417 | 0.607 |
| 3 | #411 | 0.382 |
| 4 | #443 | 0.374 |
| 5 | #405 | 0.329 |

The summaries of comments in Table 1 are as follows.
Intuitively, #411 seems to be the most influential comment because #411 had the most replies in Fig.1. However, considering the context of the comment-chain, the influence of #411 was certainly less than #445 and #417. Similarly, #443 and #405 were influential in that their topics dominated the following context. From these considerations, we can understand that comments of high influential value supplied influential topics which attract peoples' interest and trigger peoples' comments.
In this paper, we proposed a method for mining the archives of a mailing list by IDM, and confirmed the effectiveness by experiments. In the next work, we plan to analyze the human relationship in a mailing list by IDM to understand human roles in the community.